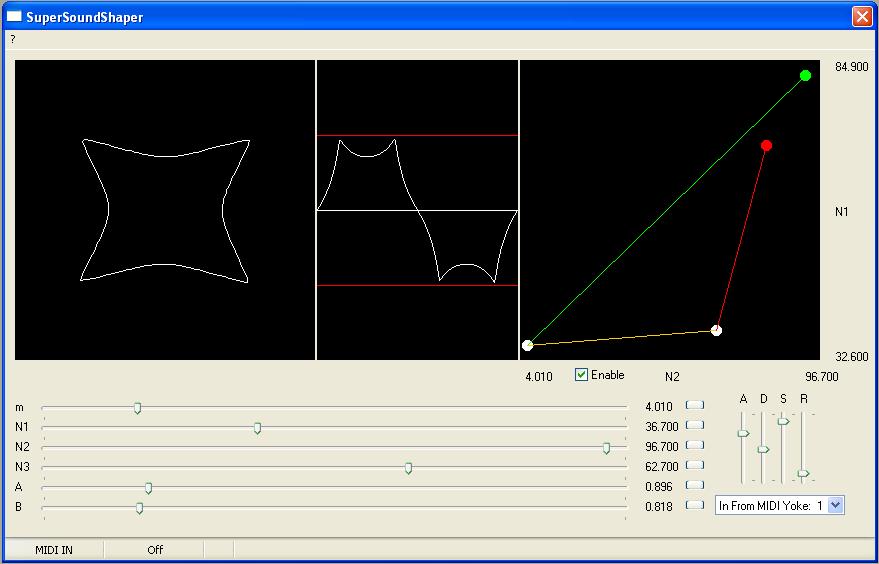
SuperSoundShaper
SuperSoundShaper is a polar-to-rectangular sound synthesizer, capable not only of producing a wide variety of polar plot 'shapes' - and corresponding sound waveforms - but also seamlessly morphing from one set to another. And of course it is playable in real-time with a midi keyboard.
SuperSoundShaper Download
| supersoundshaperv101install.zip | |
| File Size: | 134 kb |
| File Type: | zip |
Simply unzip the contents of this file into any directory on your hard drive, and double-click on 'SuperSoundShaperv101.exe' to launch the application.
System Requirements
Minimum Hardware: Intel Pentium 2, 500MHz. 512MB RAM
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Background
In polar-to-rectangular synthesis, we take the plot of a function expressed in polar coordinates (radius r from the origin as a function of angle θ), and have it drive the amplitude of a sound waveform, given by:
y = r*sin(θ), since in 'rectangular' form, a vector's length and direction are expressed in terms of its vertical and horizontal span.
y = r*sin(θ), since in 'rectangular' form, a vector's length and direction are expressed in terms of its vertical and horizontal span.
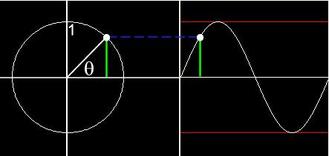
Here we have the waveform for a very simple polar plot - that of a unit circle. Since r = 1, a sine wave is swept out by y = sin(θ) as θ rotates counter-clockwise from 0 to 2π.
But what if our polar plot is that of say an ellipse instead of a circle? We would then expect to see the sine wave skew as we 'stretch' and 'squash' the ellipse. Here are two different ways I obtained the polar plot of an ellipse:
Ellipse Polar Plot - Method 1
The parametric equations (x and y co-ordinates written in terms of t) of an ellipse are given as:
x = a*cos(t)
y = b*sin(t)
But we want x and y in terms of the polar angle θ
Now, θ = atan(y/x)
So:
θ = atan(b*sin(t)/a*cos(t))
θ = atan((b/a)*tan(t))
tan(θ) = (b/a)*tan(t)
(a/b)*tan(θ) = tan(t)
atan((a/b)*tan(θ)) = t
Substituting t into the parametric equations, we get:
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
But atan only works in the range -π/2<θ<π/2
So for the complete 0 to 2π rotation, we have to 'reflect' the above segment into each quadrant, to form an ellipse. Which means, we do this:
0<=θ<π/2
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
θ = π/2
x = 0
y = b
π/2<θ<3π/2
θ = θ - π
x = a*cos(atan((a/b)*tan(θ)))*-1
y = b*sin(atan((a/b)*tan(θ)))*-1
θ = 3π/2
x = 0
y = -b
3π/2<θ<=2π
θ = θ - 2π
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
x = a*cos(t)
y = b*sin(t)
But we want x and y in terms of the polar angle θ
Now, θ = atan(y/x)
So:
θ = atan(b*sin(t)/a*cos(t))
θ = atan((b/a)*tan(t))
tan(θ) = (b/a)*tan(t)
(a/b)*tan(θ) = tan(t)
atan((a/b)*tan(θ)) = t
Substituting t into the parametric equations, we get:
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
But atan only works in the range -π/2<θ<π/2
So for the complete 0 to 2π rotation, we have to 'reflect' the above segment into each quadrant, to form an ellipse. Which means, we do this:
0<=θ<π/2
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
θ = π/2
x = 0
y = b
π/2<θ<3π/2
θ = θ - π
x = a*cos(atan((a/b)*tan(θ)))*-1
y = b*sin(atan((a/b)*tan(θ)))*-1
θ = 3π/2
x = 0
y = -b
3π/2<θ<=2π
θ = θ - 2π
x = a*cos(atan((a/b)*tan(θ)))
y = b*sin(atan((a/b)*tan(θ)))
Ellipse Polar Plot - Method 2
An ellipse centred at (0,0) is described by the following cartesian equation:
(x^2/a^2) + (y^2/b^2) = 1
Now, we know that we do as follows to convert from polar to rectangular co-ordinates:
y = r*sin(θ)
x = r*cos(θ)
We want r as a function of θ (so then for the complete 0 to 2π rotation, we can easily determine x and y)
Substituting for x and y in the cartesian equation:
((r^2)*cos^2(θ)/(a^2)) + ((r^2)*sin^2(θ)/(b^2)) = 1
((r^2)/((a^2)*(b^2)))*((b^2)*cos^2(θ) + (a^2)*sin^2(θ)) = 1
(r^2)*((b^2)*cos^2(θ) + (a^2)*sin^2(θ)) = (a^2)*(b^2)
Thus: r = (a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5)
So we have:
0<=θ<=2π
x = ((a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5))*cos(θ)
y = ((a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5))*sin(θ)
(x^2/a^2) + (y^2/b^2) = 1
Now, we know that we do as follows to convert from polar to rectangular co-ordinates:
y = r*sin(θ)
x = r*cos(θ)
We want r as a function of θ (so then for the complete 0 to 2π rotation, we can easily determine x and y)
Substituting for x and y in the cartesian equation:
((r^2)*cos^2(θ)/(a^2)) + ((r^2)*sin^2(θ)/(b^2)) = 1
((r^2)/((a^2)*(b^2)))*((b^2)*cos^2(θ) + (a^2)*sin^2(θ)) = 1
(r^2)*((b^2)*cos^2(θ) + (a^2)*sin^2(θ)) = (a^2)*(b^2)
Thus: r = (a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5)
So we have:
0<=θ<=2π
x = ((a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5))*cos(θ)
y = ((a*b)/(((b^2)*cos^2(θ) + (a^2)*sin^2(θ))^0.5))*sin(θ)
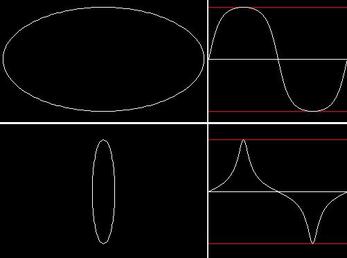
Using either of the ellipse polar plot methods above, if we set:
a = b = 1
we are back to our circle polar plot and sine wave.
But by varying a (leaving b = 1 as our maximum waveform amplitude), the waveform becomes 'flatter' as the ellipse 'stretches' and 'pointier' as the ellipse 'squashes'.
a = b = 1
we are back to our circle polar plot and sine wave.
But by varying a (leaving b = 1 as our maximum waveform amplitude), the waveform becomes 'flatter' as the ellipse 'stretches' and 'pointier' as the ellipse 'squashes'.
Why stop here though?
Super-Ellipse
A so-called Super-Ellipse, gives us one more degree of freedom. Its cartesian equation is:
|(x^2/a^n)| + |(y^2/b^n)| = 1
Here n is a variable (which need not be a whole number of course), unlike the situation with an ellipse where n = 2
The polar form (r as a function of θ) in this case can be written as:
r = (((Abs(a*cos(θ)))^n) + ((Abs(b*sin(θ)))^n)) ^ (-1/n)
|(x^2/a^n)| + |(y^2/b^n)| = 1
Here n is a variable (which need not be a whole number of course), unlike the situation with an ellipse where n = 2
The polar form (r as a function of θ) in this case can be written as:
r = (((Abs(a*cos(θ)))^n) + ((Abs(b*sin(θ)))^n)) ^ (-1/n)
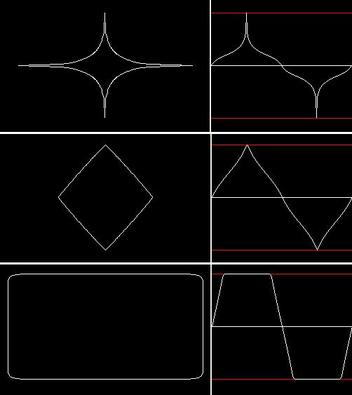
Varying n distorts the polar plot from an ellipse to that of other shapes, and this has a corresponding effect on our waveform. For example, the Super-Ellipse makes 'pinched dome', triangular and 'flat topped' waveforms all possible.
But we can go beyond even the Super-Ellipse!
Super-Formula
The Super-Forumla is a generalization of the Super-Ellipse, and gives us a total of six variables to play with. It was evolved by Belgian Botanist Johan Gielis, in his quest to find a forumla which could describe biological forms. The Super-Formula is capable of producing a wide variety of natural shapes - polygons, starfish, petals, snowflakes and so on. Since the Super-Formula generalizes the Super-Ellipse, in a sense any closed curve can be regarded as some sort of deformed ellipse!
The Super-Formula is expressed as:
r = (((Abs(a*cos(m*θ/4)))^n2) + ((Abs(b*sin(m*θ/4)))^n3)) ^ (-1/n1)
The Super-Formula is expressed as:
r = (((Abs(a*cos(m*θ/4)))^n2) + ((Abs(b*sin(m*θ/4)))^n3)) ^ (-1/n1)
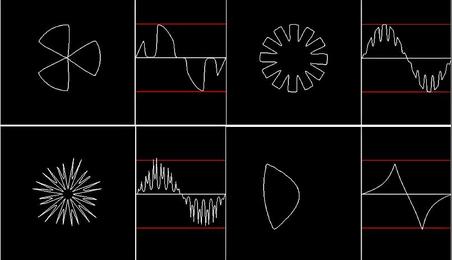
Which gives us these kinds of additional polar plot and waveform possibilities. SuperSoundShaper uses the Super-Formula, and lets you vary the value of any two of the six parameters against each other as you play a note from a keyboard, which dynamically changes the timbre of the sound in interesting ways.