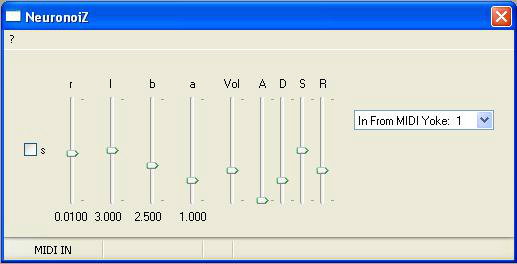
NeuronoiZ
Another fascinating method of sound synthesis is the 'sonification' of any natural process that displays periodicity. There are plenty of physical, chemical, biological etc processes like this - examples include coupled chemical reactions, geothermal eruptions, earthquakes, cyclical populations of predator and prey animals, and firing nerve cells.
Typically these processes are described by a differential equation or system of differential equations which are difficult, if not impossible, to find exact solutions to. For the purpose of 'listening to the processes' however, approximate solutions involving numerical methods are sufficient.
The 'sound of a firing nerve cell' is a concept which captured my imagination immediately, so that's what I've explored here. The result - NeuronoiZ
Typically these processes are described by a differential equation or system of differential equations which are difficult, if not impossible, to find exact solutions to. For the purpose of 'listening to the processes' however, approximate solutions involving numerical methods are sufficient.
The 'sound of a firing nerve cell' is a concept which captured my imagination immediately, so that's what I've explored here. The result - NeuronoiZ
NeuronoiZ Download
| neuronoizv101install.zip | |
| File Size: | 112 kb |
| File Type: | zip |
Simply unzip the contents of this file into any directory on your hard drive, and double-click on 'neuronoizv101.exe' to launch the application.
System Requirements
Minimum Hardware: Intel Pentium 2, 500MHz. 512MB RAM
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Doing The Neuron Dance
|
In our nervous systems - which consists of the brain, spinal cord and nerves connecting these to every other part of the body - are billions of nerve cells, or neurons. These 'excitable cells' respond to stimuli, conduct impulses, and communicate with each other. They do this through a potential established across the cell membrane, resulting from an unequal distribution of ions (charged atoms) on the two sides of the membrane.
|
An action potential is a rapid rise-fall change in membrane potential that occurs when a membrane is stimulated. Action potentials are commonly referred to as 'nerve impulses' or 'spikes', and a sequence of these is a 'spike train'. Actually, there are two main types of action potentials: one type is generated by voltage-gated sodium ion channels, the other by voltage-gated calcium channels. The former usually lasts under a millisecond (these are 'fast ion' channels) whereas the latter may last for 100 milliseconds or longer (these being 'slow ion' channels).
Bursting is where a neuron repeatedly fires discrete groups or clusters of spikes. The 'slow ion' channels (the slower calcium spikes) provide the driving force for a long burst of rapidly emitted sodium spikes. Each such burst is followed by a period of 'rest' before the next burst occurs. A burst of two spikes is called a doublet, three spikes is a triplet etc.
Bursts are thought to play an important role in communication between neurons - they may be more reliable than single spikes in evoking responses, they may carry more information content than single spikes, or actually encode different features of sensory input.
The Hindmarsh–Rose model of neuron activity was developed to simulate the spiking-bursting behaviour of the membrane potential observed in a single neuron.
Let's say the membrane potential is x(t).
The transport of ions through the 'fast ion' channels and its rate is measured by y(t): the spiking variable.
The transport of ions through the 'slow ion' channels is determined by z(t): the bursting variable.
The Hindmarsh–Rose model expresses three differential equations on these variables as follows:
dx/dt = y - a*(x^3) + b*(x^2) - z + i
dy/dt = c - d*(x^2) - y
dz/dt = r*(s*(x + 1.6) - z)
Where i is the stimulating current that enters the neuron. In the literature, the other parameter values are typically given as a = 1, b = 3, c = 1, d = 5, s = 4 and 0.001<r<0.01
So, how do we get a plot of x over time? Well, as mentioned previously, we can use a numeric method, and the Euler algorithm for solving differential equations is probably the simplest of these. It can be expressed as follows:
x(n+1) = x(n) + h*f(x(n), y(n))
Where time t moves forward in steps of h. The approximation is improved as the step size is reduced.
In NeuronoiZ, h is derived from the frequency of the note being played on the keyboard (and is in the region of 0.04 for middle C).
Applying this technique to our Hindmarsh-Rose equations, with initial values as x0 = 0, y0 = 0, z0 = 0, we evaluate the following at each iteration:
xval = x0 + h*(y0 - (x0^3) + 3*(x0^2) - z0 + i)
yval = y0 + h * (1 - 5*(x0^2) - y0)
zval = z0 + h * (0.01* ((4*(x0 + 1.6)) - z0))
x0 = xval
y0 = yval
z0 = zval
And we output xval as the value for each sample of our waveform.
But since our interest is in sound synthesis, there's no reason why we shouldn't vary some of the 'typical' parameter values to see what effect they have on the output - even if the result falls outside the scope of observed neuron behaviour!
Bursting is where a neuron repeatedly fires discrete groups or clusters of spikes. The 'slow ion' channels (the slower calcium spikes) provide the driving force for a long burst of rapidly emitted sodium spikes. Each such burst is followed by a period of 'rest' before the next burst occurs. A burst of two spikes is called a doublet, three spikes is a triplet etc.
Bursts are thought to play an important role in communication between neurons - they may be more reliable than single spikes in evoking responses, they may carry more information content than single spikes, or actually encode different features of sensory input.
The Hindmarsh–Rose model of neuron activity was developed to simulate the spiking-bursting behaviour of the membrane potential observed in a single neuron.
Let's say the membrane potential is x(t).
The transport of ions through the 'fast ion' channels and its rate is measured by y(t): the spiking variable.
The transport of ions through the 'slow ion' channels is determined by z(t): the bursting variable.
The Hindmarsh–Rose model expresses three differential equations on these variables as follows:
dx/dt = y - a*(x^3) + b*(x^2) - z + i
dy/dt = c - d*(x^2) - y
dz/dt = r*(s*(x + 1.6) - z)
Where i is the stimulating current that enters the neuron. In the literature, the other parameter values are typically given as a = 1, b = 3, c = 1, d = 5, s = 4 and 0.001<r<0.01
So, how do we get a plot of x over time? Well, as mentioned previously, we can use a numeric method, and the Euler algorithm for solving differential equations is probably the simplest of these. It can be expressed as follows:
x(n+1) = x(n) + h*f(x(n), y(n))
Where time t moves forward in steps of h. The approximation is improved as the step size is reduced.
In NeuronoiZ, h is derived from the frequency of the note being played on the keyboard (and is in the region of 0.04 for middle C).
Applying this technique to our Hindmarsh-Rose equations, with initial values as x0 = 0, y0 = 0, z0 = 0, we evaluate the following at each iteration:
xval = x0 + h*(y0 - (x0^3) + 3*(x0^2) - z0 + i)
yval = y0 + h * (1 - 5*(x0^2) - y0)
zval = z0 + h * (0.01* ((4*(x0 + 1.6)) - z0))
x0 = xval
y0 = yval
z0 = zval
And we output xval as the value for each sample of our waveform.
But since our interest is in sound synthesis, there's no reason why we shouldn't vary some of the 'typical' parameter values to see what effect they have on the output - even if the result falls outside the scope of observed neuron behaviour!
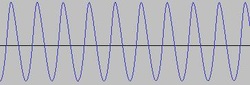
When i is high, we get something close to a sine wave. Here is x vs t for i = 20.
However our ambitions go beyond a simple sine wave, and as i drops, we get to the 'business end' of matters:

Reducing i results in a spike train.
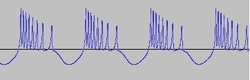
Reducing i further gives us a bursting sequence.
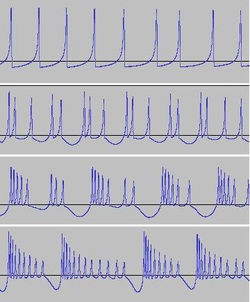
The transition from spiking to bursting is chaotic. You can see here fluctuations occurring in spike period, spike counts per burst, and burst period. Such chaos adds an additional dimension to the sound produced.
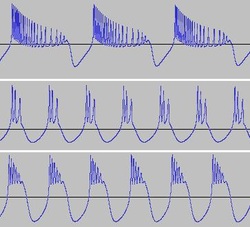
Varying i together with some of the other parameters such as r, s and b, changes spike train frequency, produces different 'spike counts per burst' and alters the 'burst shape'.