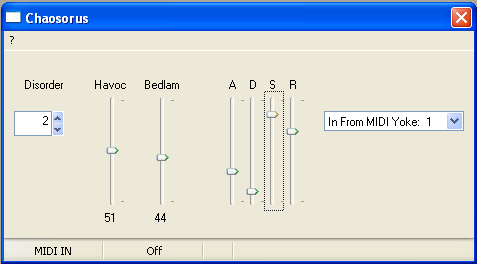
Chaosorus
Upon hearing the word 'chaos', one might imagine this scene. Or my local fruit and vegetable market at around 3.30pm on a Sunday.
But in science, chaos refers to the generation of unpredictable behaviour from a simple rule or expression (as it turns out, sometimes an alarmingly simple one). Furthermore the rule or expression has no randomness 'built in' (unlike for example the stochastic synthesis method used in Blowfly where the positions of points in the next waveform cycle are determined by probability distributions). Chaosorus features sound production through the distortion of the phase of an oscillator by such expressions.
The amazing thing is there is no pre-programmed sequencing of notes, arpeggiation, midi note sliding etc going on here!
Download Chaosorus
| chaosorusv101install.zip | |
| File Size: | 113 kb |
| File Type: | zip |
Simply unzip the contents of this file into any directory on your hard drive, and double-click on 'chaosorusv101.exe' to launch the application.
System Requirements
Minimum Hardware: Intel Pentium 2, 500MHz. 512MB RAM
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Beauty In Chaos
A chaotic process is 'deterministic' - which means where it goes next is determined by the initial conditions. It is just that with repeated application of the rule or expression, the long term behaviour becomes quite complicated - unpredictability 'emerges' over time. After a few iterations, measurements of the current state of such a process become useless indicators of where it will be, thanks to the ultra-sensitivity to the initial conditions. Even starting from extremely close initial conditions a chaotic process diverges exponentially to different states.
So whereas in everyday language people tend to use 'chaotic' and 'random' interchangeably - or at best 'chaos' as any situation displaying an apparent 'lack of order' - technically speaking deterministic chaos is not random, quite ordered and even predictable on short time scales.
The NeuronoiZ synth demonstrates how coupled differential equations in three variables can generate chaos for certain values of the coefficients. But even a very simple difference equation in one variable can generate chaos. Take the 'circle map' or 'map of the circle onto itself', which is often expressed as follows in the literature:
θ(n+1) = (θ(n) + Ω - (K/2π )*sin(2πθ(n))) mod 1
where the 'mod 1' ensures the value of θ lies between 0 and 1. Ω is the 'driving phase', which can be interpreted as the frequency. K is the 'coupling strength'. If K=0, θ is simply a rotation by 2πΩ radians.
So, this expression can be interpreted to be the phase of a sine oscillator that is perturbed by a very simple function: (K/2π )*sin(2πθ).
Again in the literature, treatment of circle maps is typically accompanied with diagrams of 'Arnold tongues' and 'Devils staircases', but we won't concern ourselves with these, as our focus is simply to get the circle map to sound for us. Now in the section Synthesis for Developers, we express a sine oscillator as:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + Phase_Add
If Phase > 1 then Phase = Phase - 1
Next T
where Phase_Add = F/SR is the incremental value which determines the frequency of the waveform. The phase plot in this case ie Phase vs T, looks like a sawtooth - it ramps linearly from 0 to 1, at which point it drops to 0 and ramps back up again. So if we place the circle map expression in this context, Phase_Add is effectively Ω - (K/2π )*sin(2πθ). Our oscillator thus becomes:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + Omega - (K/Pi2)*sin(Pi2*Phase))
If Phase > 1 then Phase = Phase - 1
Next T
Alternatively, if we use the circle map expression with the 'mod 1' in it as it appears in the literature, our oscillator is:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Mod((Phase + Omega - (K/Pi2)*sin(Pi2*Phase))), 1)
Next T
So whereas in everyday language people tend to use 'chaotic' and 'random' interchangeably - or at best 'chaos' as any situation displaying an apparent 'lack of order' - technically speaking deterministic chaos is not random, quite ordered and even predictable on short time scales.
The NeuronoiZ synth demonstrates how coupled differential equations in three variables can generate chaos for certain values of the coefficients. But even a very simple difference equation in one variable can generate chaos. Take the 'circle map' or 'map of the circle onto itself', which is often expressed as follows in the literature:
θ(n+1) = (θ(n) + Ω - (K/2π )*sin(2πθ(n))) mod 1
where the 'mod 1' ensures the value of θ lies between 0 and 1. Ω is the 'driving phase', which can be interpreted as the frequency. K is the 'coupling strength'. If K=0, θ is simply a rotation by 2πΩ radians.
So, this expression can be interpreted to be the phase of a sine oscillator that is perturbed by a very simple function: (K/2π )*sin(2πθ).
Again in the literature, treatment of circle maps is typically accompanied with diagrams of 'Arnold tongues' and 'Devils staircases', but we won't concern ourselves with these, as our focus is simply to get the circle map to sound for us. Now in the section Synthesis for Developers, we express a sine oscillator as:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + Phase_Add
If Phase > 1 then Phase = Phase - 1
Next T
where Phase_Add = F/SR is the incremental value which determines the frequency of the waveform. The phase plot in this case ie Phase vs T, looks like a sawtooth - it ramps linearly from 0 to 1, at which point it drops to 0 and ramps back up again. So if we place the circle map expression in this context, Phase_Add is effectively Ω - (K/2π )*sin(2πθ). Our oscillator thus becomes:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + Omega - (K/Pi2)*sin(Pi2*Phase))
If Phase > 1 then Phase = Phase - 1
Next T
Alternatively, if we use the circle map expression with the 'mod 1' in it as it appears in the literature, our oscillator is:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Mod((Phase + Omega - (K/Pi2)*sin(Pi2*Phase))), 1)
Next T
In Chaosorus, I build on this foundation as follows. Let Delta = F/SR (where F = frequency of the note being played on the keyboard), and s>0:
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + (Delta + Omega) - (K/Pi2)*sin(Pi2*Phase))
Phase = Phase + Delta + Mod((s*Phase), 1)
If Phase > 1 then Phase = Phase - 1
Next T
The Phase value determined from the circle map is fed into yet another simple chaotic function (note that when s = 2, this second function is a 'doubling' or 'dyadic' map). Varying s gives us another dimension for our sound shaping. The Delta is simply an increment added to the initial condition set by Omega, so that as one plays up and down the keyboard, one is greeted with a different soundset at each key. Also since Omega can be a large fraction of the Sampling Rate (up to Nyquist or 0.5*SR in fact), I've employed a low Sampling Rate in Chaosorus to keep things in the audible range.
The results of this are intriguing, and include:
1. 'Rhythmic Noise' or 'Noise with underlying sub-patterns': sometimes the noise sounds like it is being dynamically filtered, or mixed with tones of discernible frequencies. Very suggestive of 'industrial' sounds like engines, turbines, steam valves, stamping machines, presses, explosions.
2. Single wave-shaped notes sometimes accompanied with pitch glide/bending and sometimes without, sometimes locking to certain frequencies and sometimes sounding like they have been treated with a variety of effects such as reverb, delay, flanger etc.
3. Short melody segments getting played by 'instruments' which sometimes sound like bagpipes or shehnai (Indian double reed oboe), and which emerge and disappear or morph into each other.
4. Long note sequences which keep evolving as long as the key is pressed.
Each key produces something different even on the same overall settings of Omega, K and s (Havoc, Bedlam and Disorder on the GUI respectively), but the great thing is that if you like what you hear, you can always repeat it by pressing the same key again!
For T = 0 to L
O = A*(sin(Pi2*Phase))
Phase = Phase + (Delta + Omega) - (K/Pi2)*sin(Pi2*Phase))
Phase = Phase + Delta + Mod((s*Phase), 1)
If Phase > 1 then Phase = Phase - 1
Next T
The Phase value determined from the circle map is fed into yet another simple chaotic function (note that when s = 2, this second function is a 'doubling' or 'dyadic' map). Varying s gives us another dimension for our sound shaping. The Delta is simply an increment added to the initial condition set by Omega, so that as one plays up and down the keyboard, one is greeted with a different soundset at each key. Also since Omega can be a large fraction of the Sampling Rate (up to Nyquist or 0.5*SR in fact), I've employed a low Sampling Rate in Chaosorus to keep things in the audible range.
The results of this are intriguing, and include:
1. 'Rhythmic Noise' or 'Noise with underlying sub-patterns': sometimes the noise sounds like it is being dynamically filtered, or mixed with tones of discernible frequencies. Very suggestive of 'industrial' sounds like engines, turbines, steam valves, stamping machines, presses, explosions.
2. Single wave-shaped notes sometimes accompanied with pitch glide/bending and sometimes without, sometimes locking to certain frequencies and sometimes sounding like they have been treated with a variety of effects such as reverb, delay, flanger etc.
3. Short melody segments getting played by 'instruments' which sometimes sound like bagpipes or shehnai (Indian double reed oboe), and which emerge and disappear or morph into each other.
4. Long note sequences which keep evolving as long as the key is pressed.
Each key produces something different even on the same overall settings of Omega, K and s (Havoc, Bedlam and Disorder on the GUI respectively), but the great thing is that if you like what you hear, you can always repeat it by pressing the same key again!