Garble Marvel
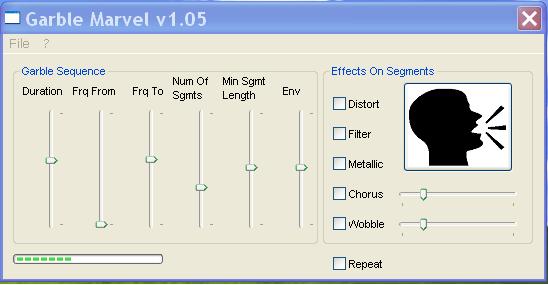
Although the FlexibeatzII application contains tools to process your voice to sound like a robot, it needs a sample of your speech or singing to do so. I created Garble Marvel to allow the computer itself to generate a variable sequence of voice-like utterances for you, which you can directly incorporate in your music! Record its output to a .wav file, open it in FlexibeatzII and you've got yourself a bizarre synthetic 'vocalist' for your fully synthetic compositions (that is, if you choose to synthesize all the other instruments as well). But you can of course use Garble Marvel's output in any DAW, sampler or audio sequencer since it is a completely independent, stand-alone application.
Here's a short video of Garble Marvel in action:
Garble Marvel Portable Application Description File
'PAD' files are datasets which allow software authors to communicate specific and most often requested information about their products to online communities in a concise and standard way. This PAD file is in XML format (data can be extracted and parsed using standard XML toolkits):
| garblemarvel.xml | |
| File Size: | 13 kb |
| File Type: | xml |
Garble Marvel Download
| garblemarvel105.zip | |
| File Size: | 122 kb |
| File Type: | zip |
Simply unzip the contents of this file into any directory on your hard drive, and double-click on 'garblemarvel105.exe' to launch the application.
System Requirements
Minimum Hardware: Intel Pentium 2, 500MHz. 512MB RAM
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Operating System: Windows 2000, XP, 7. I have successfully installed and run the application on these platforms, but should also work with Windows Vista.
Garble Marvel's Sound Engine
Garble Marvel uses 'formant synthesis' to create the speech-like sounds. The human voice is basically an acoustic pressure wave created when air is expelled from the lungs through the vocal tract, and as the wave passes through this, its spectrum is altered by the resonances of the vocal tract. Peaks are produced in the spectrum as a result of concentration of acoustic energy around particular frequencies - called formants.
The distinctiveness of the vowel sounds can be attributed to the differences in their first three formant frequencies.
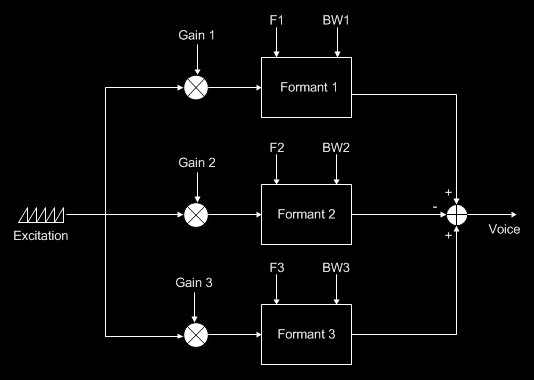
To model this, we start with an excitation signal - which can be any harmonics-rich signal like an impulse train, or as I've used, a filtered sawtooth wave at a frequency of the required pitch of the vocal sound. This is then fed, at different amplitudes, into a set of three parallel narrow band-pass filters, each tuned to a resonant frequency (formant), and the outputs combined:
The distinctiveness of the vowel sounds can be attributed to the differences in their first three formant frequencies.
To model this, we start with an excitation signal - which can be any harmonics-rich signal like an impulse train, or as I've used, a filtered sawtooth wave at a frequency of the required pitch of the vocal sound. This is then fed, at different amplitudes, into a set of three parallel narrow band-pass filters, each tuned to a resonant frequency (formant), and the outputs combined:
The great thing about this parallel structure is that it also allows control of the bandwidth of each formant individually.
Morphing from one vowel sound to another is accomplished by 'sliding' from one set of frequency and bandwidth values to another.
If we were to 'zoom into' these formant filters, we'd see that each is defined by a fairly simple difference equation. For every sample n, the output is y[n] given an input x[n], according to:
y[n] = A*x[n] + B*y[n-1] + C*y[n-2]
If we want for example frequency F1 = 310 and bandwidth BW1 = 45 at Sampling Rate = SR = 44100, each of the coefficients are calculated as follows:
C = -1 * Exp(-2 * π * BW / SR) = -1 * Exp(-2 * π * 45 / 44100) = -0.9936091
B = (2 * Exp(-1 * π * BW / SR)) * Cos(2 * π * F / SR) = (2 * Exp(-1 * π * 45 / 44100)) * Cos(2 * Pi * 310 / 44100) = 1.991655
A = 1 - C - B = 1.954436E-03
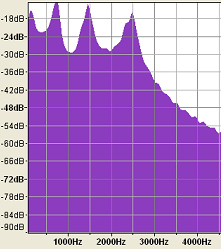
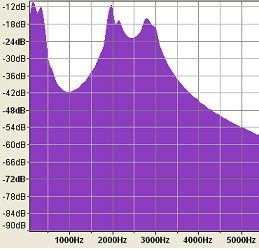
Typically for the vowel sounds, the first formant is in the range 150-850 Hz, the second in the range 500-2500 Hz and the third in the range 1500-3500 Hz. These frequency peaks are clearly visible in the following:
Morphing from one vowel sound to another is accomplished by 'sliding' from one set of frequency and bandwidth values to another.
If we were to 'zoom into' these formant filters, we'd see that each is defined by a fairly simple difference equation. For every sample n, the output is y[n] given an input x[n], according to:
y[n] = A*x[n] + B*y[n-1] + C*y[n-2]
If we want for example frequency F1 = 310 and bandwidth BW1 = 45 at Sampling Rate = SR = 44100, each of the coefficients are calculated as follows:
C = -1 * Exp(-2 * π * BW / SR) = -1 * Exp(-2 * π * 45 / 44100) = -0.9936091
B = (2 * Exp(-1 * π * BW / SR)) * Cos(2 * π * F / SR) = (2 * Exp(-1 * π * 45 / 44100)) * Cos(2 * Pi * 310 / 44100) = 1.991655
A = 1 - C - B = 1.954436E-03
Typically for the vowel sounds, the first formant is in the range 150-850 Hz, the second in the range 500-2500 Hz and the third in the range 1500-3500 Hz. These frequency peaks are clearly visible in the following: